Übungsklausur

Übungsklausur

Lösungen: (siehe unten - scrollen!)

Aufgabe 1a:

Gemeinsam: Verbindung von Punkten bzw. Funktionen mit ganzrationalen Funktionen, und zwar stetig, knickfrei und krümmungsruckfrei.

Unterschiede: Grad der Funktionen, Splines: nur Punkte werden verbunden, Splines: Krümmung an den Randpunkten in der Regel Null.

Aufgabe 1b:

Trassierung: 6 Bedingungen -> Ganzrationale Funktion 5. Grades.

3. bzw. 7. Grades bedeutete 4 bzw. 8 Bedingungen - zuwenige bzw. zuviele.

Aufgabe 1c:

Bei kubischen Splines hat man 4 Bedingungen pro verbindender Funktion, also eine ganzrationalen Funktionen 3. Grades.

Aufgabe 2a:

Aufgabe 2b:

Funktionen in den Taschenrechner unter f(x), g(x), h(x) einspeichern. Ableitungen berechnen (f1,f2,g1,g2,h1,h2). Ausrechnen:

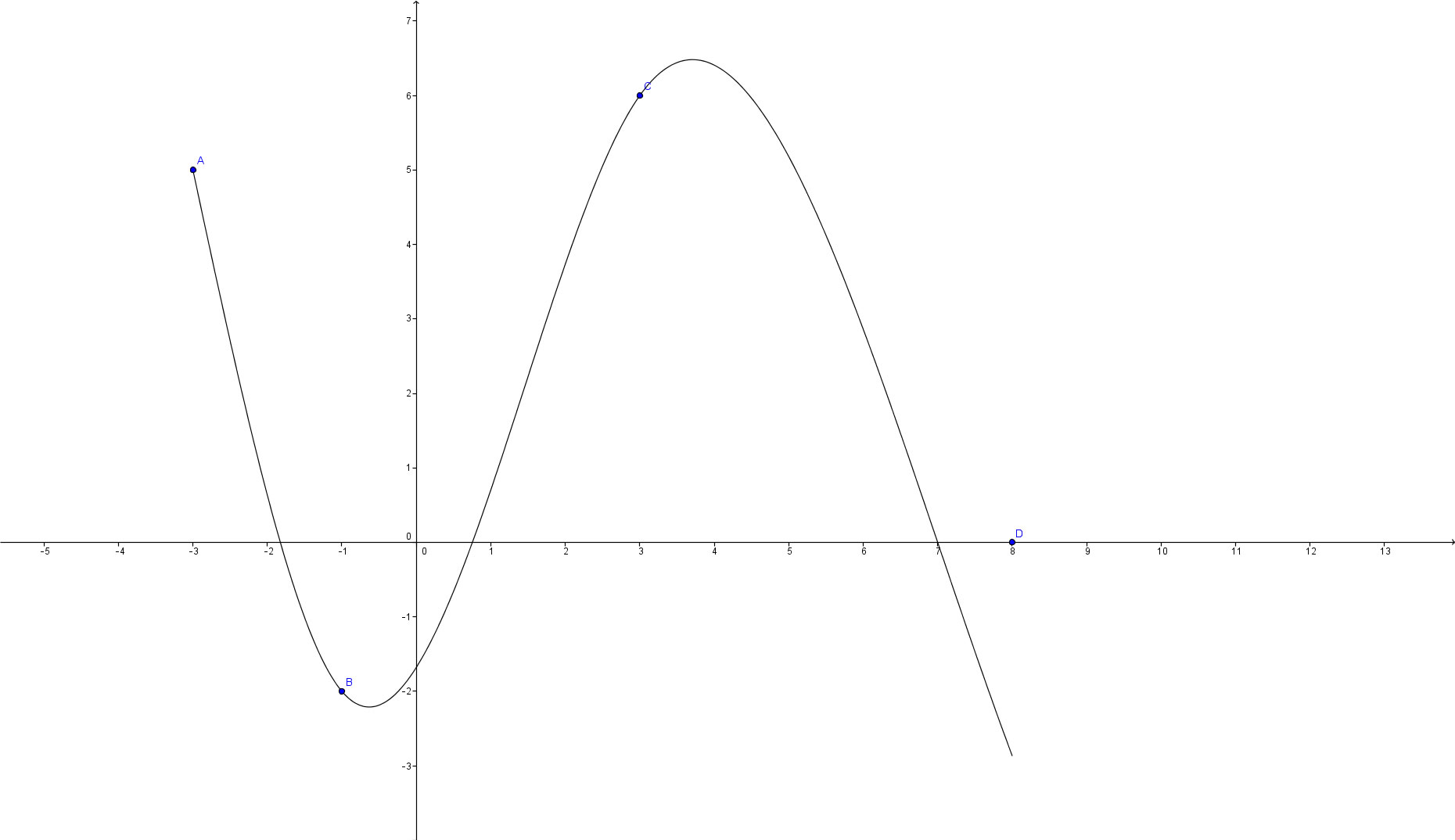
Punkt 1:

f(-3)=5 OK

f2(-3)=0 OK

Punkt 2:

f(-1)=-2 OK

g(-1)=-2 OK

f1(-1)=-13/11 und g1(-1)=-13/11 OK

f2(-1)=153/44 und g2(-1)=13/11 OK

Punkt 3:

g(3)=6 OK

h(3)=6 OK

g1(3)=31/22 und h1(3)=31/22 OK

g2(3)=-24/11 und h2(3)=-24/11 OK

Punkt 4:

h(8)=-63/22 NICHT OK

h2(8)=6/11 NICHT OK

Die Bedingungen für Punkt 4 sind nicht erfüllt!

Aufgabe 2c:

Es sieht so aus, als ob hier der Punkt (7|0) und nicht (8|0) zur Berechnung verwendet wurde. Für die linken drei Punkte sieht das Ergebnis gut aus. Der rechte passt nicht!

Aufgabe 2d:

Ändern:

f''(-3)=-1

h''(8)=2

Aufgabe 2e:

Sämtliche Splines ändern sich, da die Bedingungen alle miteinander verknüpft sind!

Aufgabe 3a:

Lösung mit der Geraden: nicht knickfrei.

Lösung mit dem Kreisbogen: nicht krümmungsruckfrei.

Aufgabe 3c:

Lösung ist z. B. die dargestellte Verbindung mit der Geraden rechts oben. Die Gleichung lautet:

y=2/7*x + 22/7. Der PKW-Fahrer muss an der Verbindungsstelle das Steuer herumreißen und wird einen Unfall bauen.

Anderes Vorgehen:

Gesucht: Funktion f(x) mit den Bedingungen:

f(-4)=2 : Stetigkeit links

f(3)=4 : Stetigkeit rechts

f''(-4)=0 : Krümmungsruckfreiheit links (2. Ableitung der Geraden ist Null)

f''(3)=0 : Krümmungsruckfreiheit rechts

Knickfreiheit soll nicht gegeben sein, d. h. die Ableitungen dürfen links nicht 1 und rechts nicht -0,5 sein. Beispielsweise setze ich:

f'(-4)=0

f'(3)=0

Jetzt hat man 6 Bedingungen und muss eine Funktions 5. Grades finden. Das schenke ich mir hier...... (Lösungsweg wurde schriftlich verteilt).